6.8 Função Deviance

\[ \begin{aligned} D(y,\hat\mu(x)) &= \sum_{i=1}^n 2\left[y_i\log\frac{y_i}{\hat\mu_i(x_i)} + (1-y_i)\log\left(\frac{1-y_i}{1-\hat\mu_i(x_i)}\right)\right] = \\ &= 2 D_{KL}\left(y||\hat\mu(x)\right), \end{aligned} \]

onde \(D_{KL}(p||q) = \sum_i p_i\log\frac{p_i}{q_i}\) é a divergência de Kullback-Leibler.

Agora, veja um modelo de deep learning:

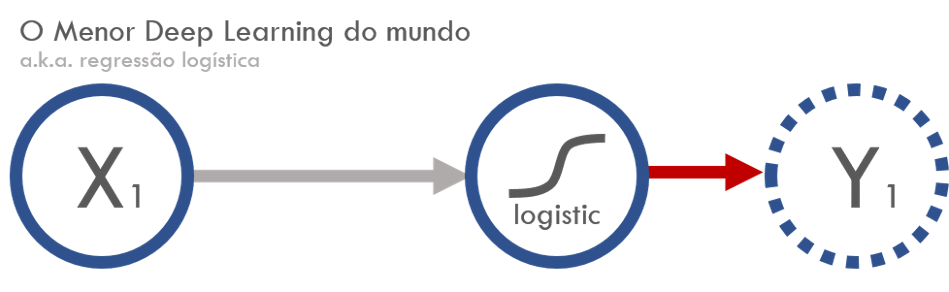
Faz uma combinação linear inputs \(x\), adiciona um viés (bias) e depois aplica uma função de ativação não linear. No nosso caso, adiciona um parâmetro multiplicando \(x\) e um viés fixo, fazendo

\[ f(x) = w x + \text{bias} \]

A função de ativação é uma sigmoide, dada por

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

Notou alguma similaridade?

6.8.1 Função de custo: categorical cross-entropy

\[ \begin{aligned} H(p, q) &= H(p) + D_{KL}(p||q) \\ &= -\sum_x p(x)\log(q(x)) \end{aligned} \]

No nosso caso, isso é equivalente a uma constante mais a função deviance.

Para ajustar os parâmetros, existem diversos algoritmos de otimização. Um dos mais utilizados é o de descida de gradiente estocástico.

6.8.2 Exemplot

logistic <- function(x) 1 / (1 + exp(-x))

n <- 100000
set.seed(19910401)
dados <- tibble(
  x = runif(n, -2, 2),
  y = rbinom(n, 1, prob = logistic(-1 + 2 * x))
)
dados

Ajustando uma regressão logística no R

modelo <- glm(y ~ x, data = dados, family = 'binomial')
broom::tidy(modelo)

Ajustando um deep learning com o keras

library(keras)
input_keras <- layer_input(shape = 1, name = "modelo_keras")

output_keras <- input_keras %>% 
  layer_dense(units = 1, name = "camada_unica") %>%
  layer_activation("sigmoid", 
                   input_shape = 1, 
                   name = "link_logistic")

# Constrói a nossa hipótese f(x) (da E[y] = f(x))
modelo_keras <- keras_model(input_keras, output_keras)

A especificação do modelo é dada por

summary(modelo_keras)

#> ___________________________________________________________________________
#> Layer (type)                     Output Shape                  Param #     
#> ===========================================================================
#> modelo_keras (InputLayer)        (None, 1)                     0           
#> ___________________________________________________________________________
#> camada_unica (Dense)             (None, 1)                     2           
#> ___________________________________________________________________________
#> link_logistic (Activation)       (None, 1)                     0           
#> ===========================================================================
#> Total params: 2
#> Trainable params: 2
#> Non-trainable params: 0
#> ___________________________________________________________________________

Agora, especificamos a função de perda e a forma de otimizar

modelo_keras %>% 
  compile(
    loss = 'binary_crossentropy',
    optimizer = "sgd"
  )

modelo_keras %>% 
  fit(x = dados$x, y = dados$y, epochs = 3)

modelo_keras %>% 
  get_layer("camada_unica") %>% 
  get_weights()

#> [[1]]
#>         [,1]
#> [1,] 2.00727
#> 
#> [[2]]
#> [1] -1.017746

Algumas dúvidas que podem surgir para você nesse momento:

• Se é a mesma coisa, por que ele está ganhando tanta popularidade?
• Devo estudar deep learning ou posso continuar fazendo regressão logística?